簡單回顧
在ML_Day2(機器學習種類)有提Regression與classificatoin的差異。所謂的線性迴歸（Linear Regression），簡單來說就是，如果我們要找的function，能夠用線性組表示，並且直接輸出一個數值。

• Example
  以神奇寶貝為例，我們要找一個function，預測神奇寶貝進化後的CP值。
  由下面片可以看到，這是一個linear model。把神奇寶貝的一些屬性，例如身高、體重、性別…等feature當作input，最後可以得到output(CP值)。
  
  

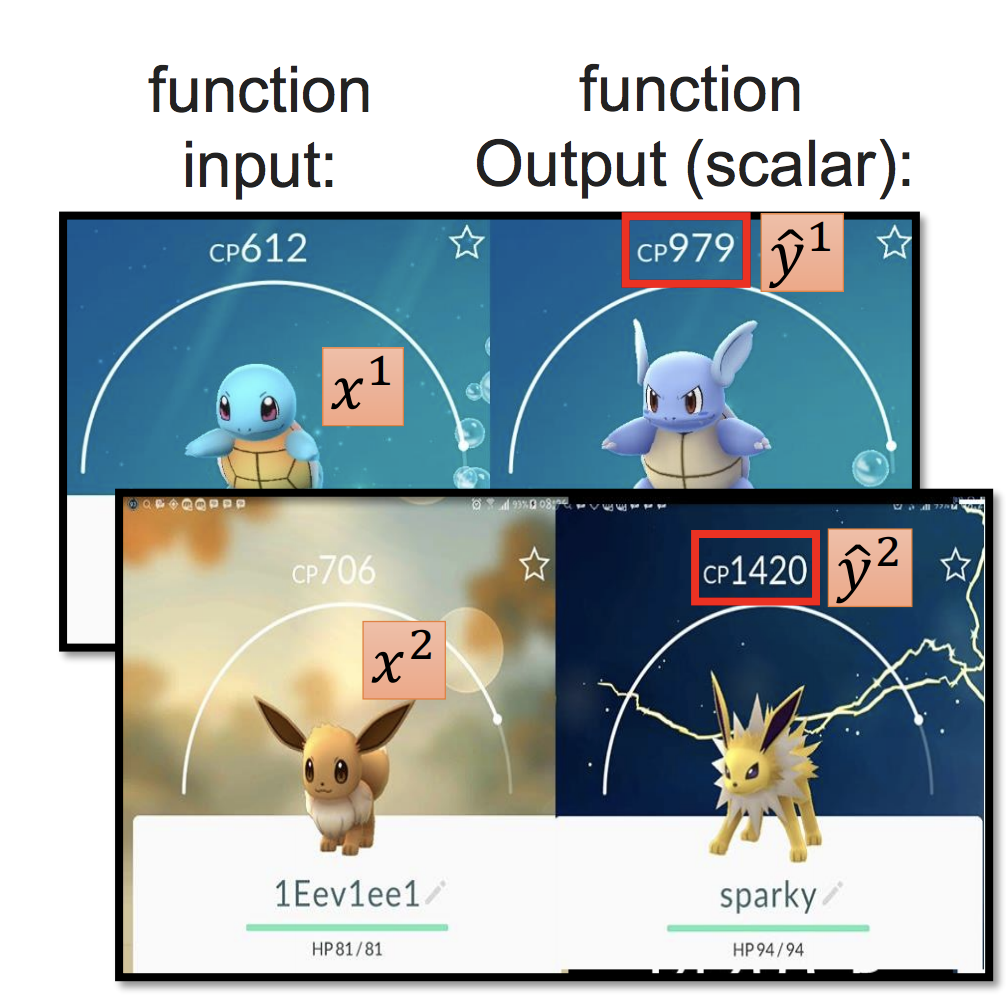
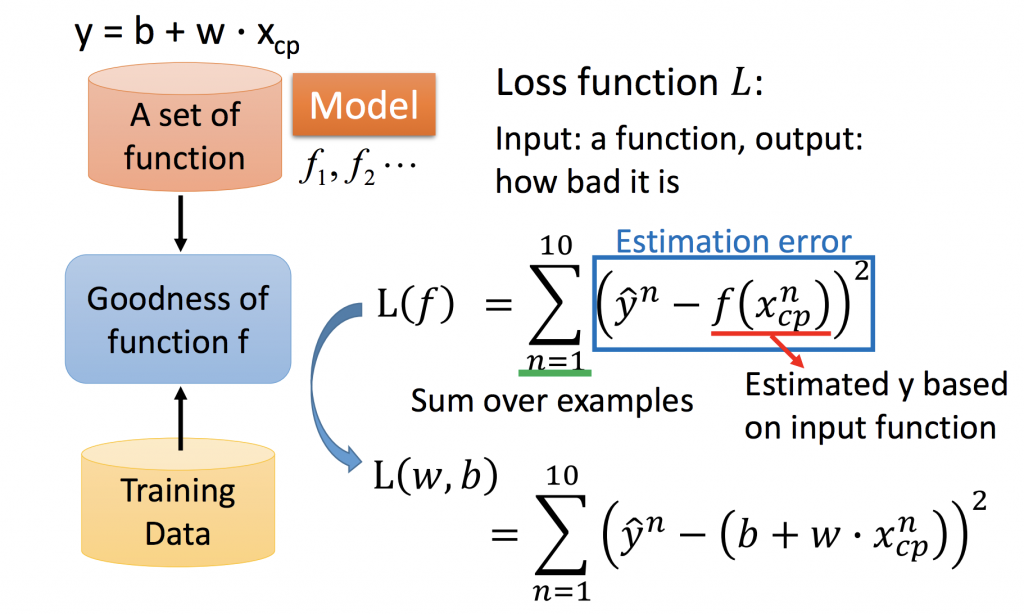
如果今天搜集十隻神奇寶貝，把每一隻的feature都進去我們的linear model做預測，我們可以得到linear regression的圖。並且希望能找到一個linear model能讓實際上與預測出來的誤差越小越好。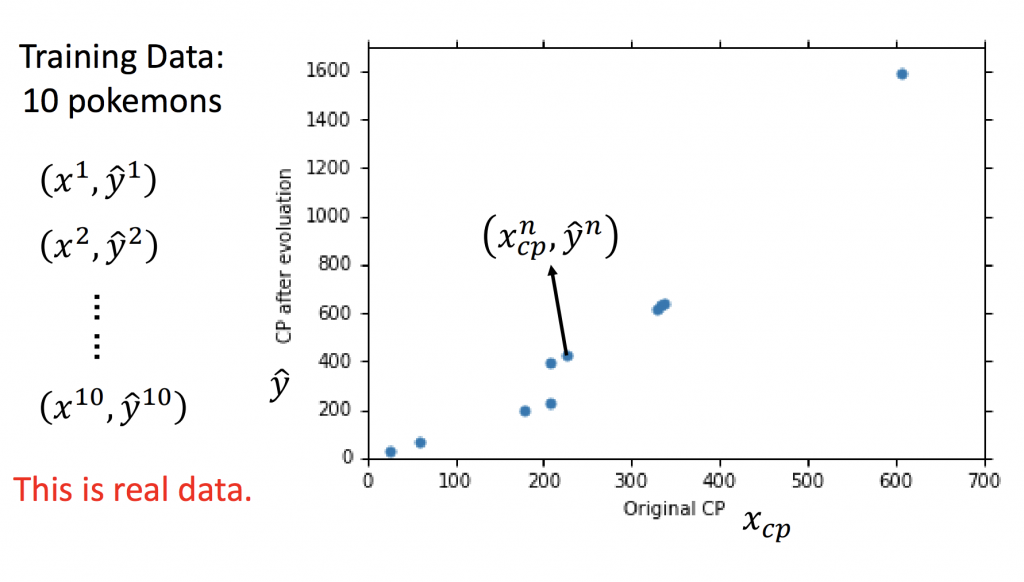

Loss Function:
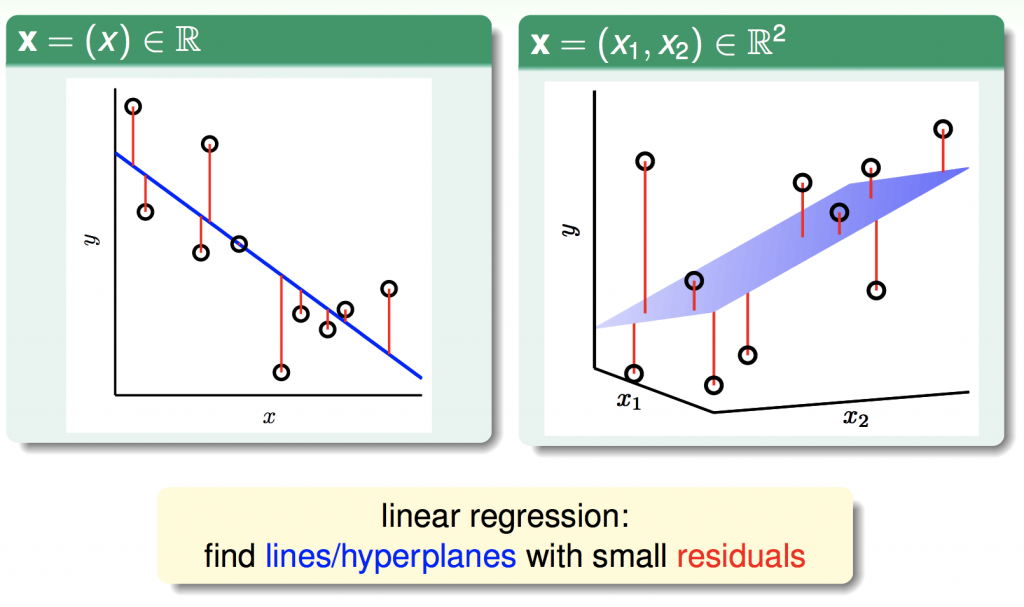
那如何找到比較好的linear model，我們希望能讓誤差越小越好。所以必須訂一個loss function來衡量參數的好壞。這邊介紹一個比較常用的方法，square error measure。如果linear model丟進去loss function的誤差越大越不好；反之，loss function的誤差越小越好。

Gradient Descent:
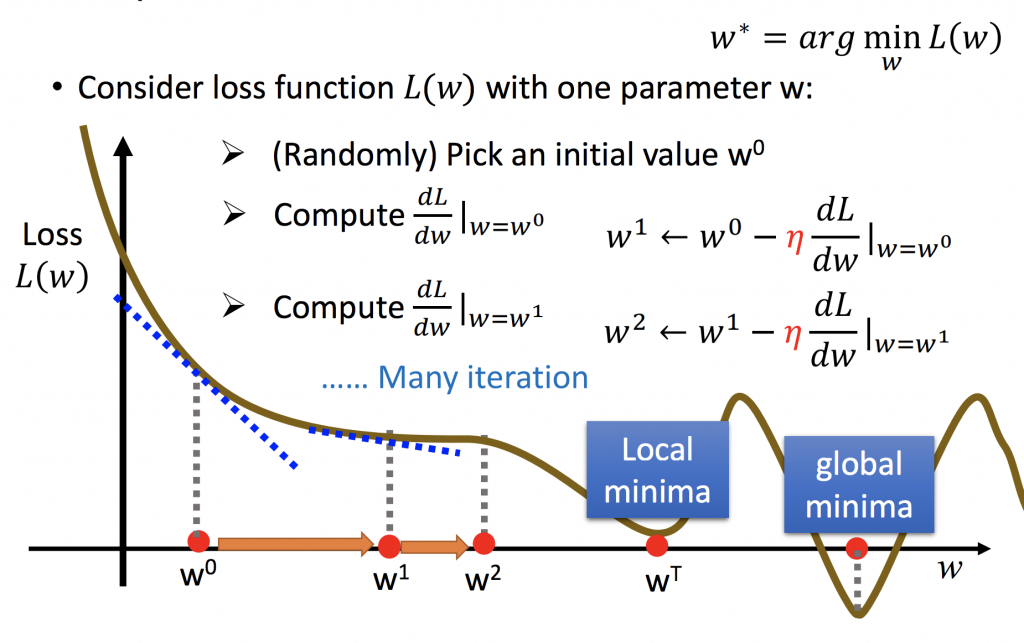
計算完loss function之後，我們要如何衡量model的好壞?上面有提到，如果loss function越小越好。以我們的function來說就是找到w、b能讓loss function最小，所以我們必須對loss function做偏微分（切線斜率）就是找極大極小值的概念，找到loss function斜率為0的地方，參數就無法再做更新了。偏微分前面有一個常數稱為learning rate，如果值越大，代表每次更新的幅度越大；反之，如果值越小，代表每次更新的幅度越小。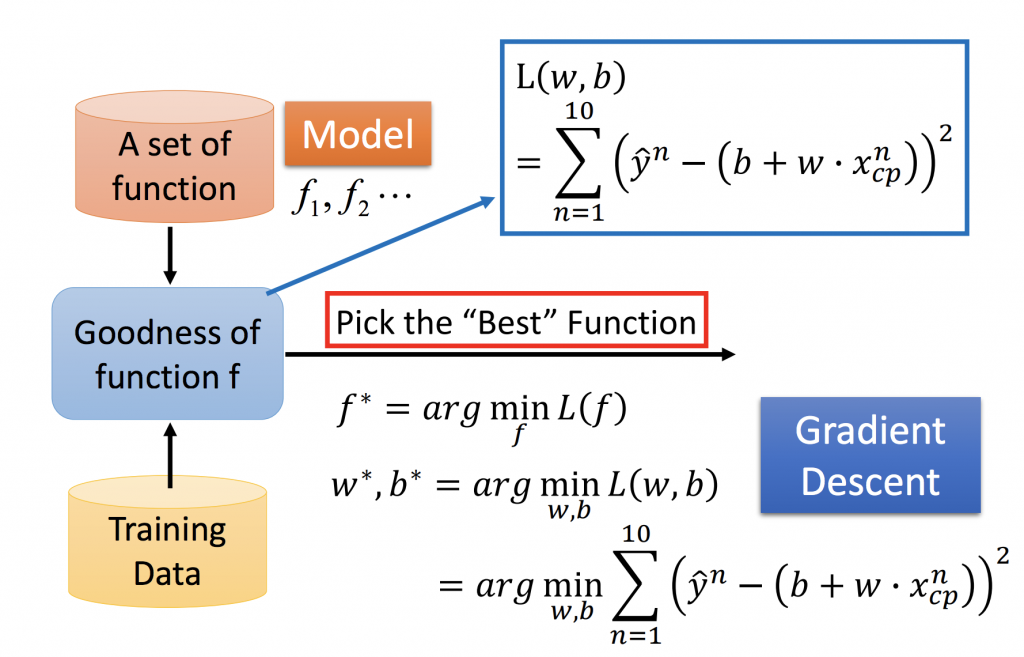

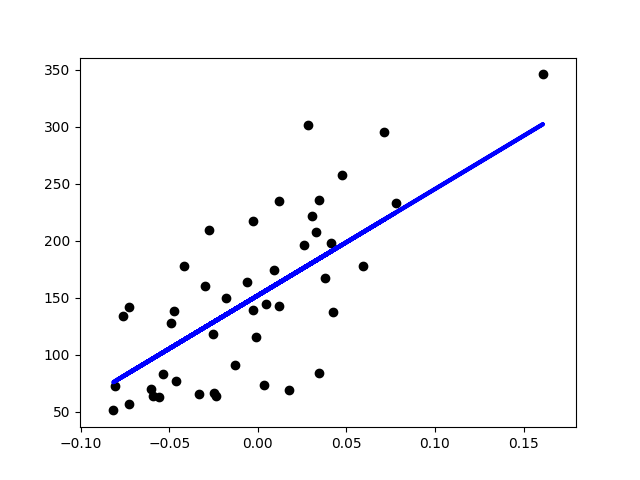
sklear-learn數據實作Linear Regression:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score, accuracy_score


def main():
    diabetes = datasets.load_diabetes()

    X = diabetes.data[:, np.newaxis, 2]
    print("Data shape: ", X.shape)  

    x_train, x_test, y_train, y_test = train_test_split(
        X, diabetes.target, test_size=0.1, random_state=4)

    regr = linear_model.LinearRegression()

    regr.fit(x_train, y_train)

    y_pred = regr.predict(x_test)

    plt.scatter(x_test, y_test, color='black')
    plt.plot(x_test, y_pred, color='blue', linewidth=3)
    plt.show()


if __name__ == '__main__':
    main()